Published on
- 1 min read
Fast modulo calculation in FrozenDictionary

While working on the FrozenDictionary article, I found several interesting implementation details worth sharing. Let’s start simple — with a faster way to compute a modulo.
As you know, the bucket index in a dictionary is calculated as hashCode % bucketsCount. In C# and many other languages, this is done using the % operator:
var bucketNum = hashCode % bucketsCount;
In general, division is slower than multiplication or bitwise operations. So here’s a faster alternative:
uint FastModLemire(uint hashcode, ulong multiplier, uint bucketsNum) =>
(uint)((((UInt128)(hashcode * multiplier)) * bucketsNum) >> 64);
The idea is: if the number of buckets is known ahead of time, you can precompute the multiplier using the formula ulong.MaxValue / bucketsNum + 1. This allows replacing division with a combination of multiplications and bit shifts.
If you’re curious about the math behind it, check out Daniel Lemire’s paper, which describes this method. For a general understanding, reading Chapters 1 and 3.2 is enough.
Both FrozenDictionary and Dictionary use a different formula, which — according to Microsoft developers — is a bit faster. Benchmark results confirm this:
uint FastModDotNet(uint hashcode, ulong multiplier, uint bucketsNum) =>
(uint)(((((multiplier * hashcode) >> 32) + 1) * bucketsNum) >> 32);

Benchmark results
Additionally, the JIT compiler can optimize classic division and replace it with a combination of multiplications and shifts — if bucketsCount is known at compile time. In such cases, the generated assembly for DefaultModConst will be identical to FastModDotNet.
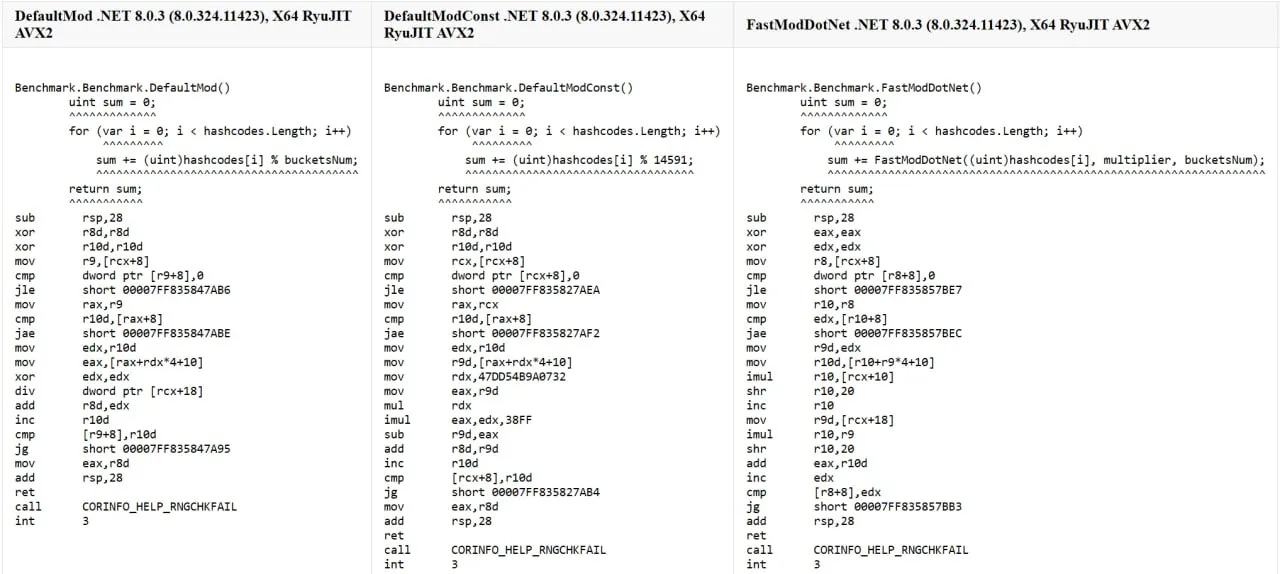
Assembly comparison for different modulo strategies
You can find the benchmark code and results on GitHub.